In the initial phase, I embarked on a series of experiments using PD (Pure Data) to analyze the input signal derived from my prototype. Here the aim was to understand how to get the parameters for the servos to tune the strings.
At first, I employed an FFT (Fast Fourier Transform) algorithm to determine the algorithm’s ability to track the pitch of the incoming signal and see how reactive and precise the analysis response while changing the tension of the strings.
To achieve that, once obtained the fundamental and the first three partials of the incoming signal, I divided the process into two steps:
- convert the difference of the estimated pitch and the incoming signal (changing the tension) into semitones:
- “Semitones = 12 * log2(frequency / referenceFrequency)”;
- attribute the estimated difference in semitones as pitch parameter of a “pitchshifter”.
The limitation:
- FFT analysis of complex signals and the latency introduced while processing the data:
- the interference between the harmonics produced by different strings can create complex frequency interactions that are not easily captured by a simple conversion method. To improve the reliability of the analysis, it would be necessary to employ more sophisticated techniques that take into account the complex harmonic relationships occurring during simultaneous string play. This could involve employing advanced signal processing algorithms or considering the specific characteristics of each string, such as its tuning, tension, and resonance properties.
The second step consisted into the application of zero crossing analysis to find the pitch of the strings. Even though I was not able to implement this process during this semester, I came out with rather interesting solutions to implement it.
First a brief introduction to the subject… In the audio domain, zero crossing[1] is an important concept that is frequently used in pitch recognition and estimation. Pitch recognition refers to the process of identifying the fundamental frequency or musical pitch of a sound.
Zero crossing analysis is employed as a technique for pitch recognition due to its effectiveness and simplicity. The fundamental frequency of a sound corresponds to the rate at which the waveform crosses the zero level. By counting the number of zero crossings within a specific time frame, it is possible to estimate the pitch of the sound.
As we traverse through the audio samples, we examine each point. If the amplitude of the current sample (N) is equal to the silent threshold and the amplitude of the following sample (N + 1) is either higher or lower than the silent threshold, then the sample point at (N) is identified as a zero-crossing point. Once we determine the number of zero crossing points, we can utilize the sampling rate of the signal and the total number of samples to calculate the duration in seconds over which these zero crossing points were counted.
The formula for this calculation is:
Number of seconds = Total number of samples / Sampling rate
Considering that each oscillation of a signal encompasses two crossings of the silent threshold, we can determine the number of oscillations by dividing the total number of zero crossing points by two.
The formula is:
Number of oscillations = Total number of zero crossing points / 2
To ascertain the frequency of the input audio signal, we employ the values obtained from steps 2 and 3. The formula for calculating the frequency in Hertz is:
Frequency of input audio signal = Number of oscillations / Number of seconds
The methodology of zero crossing analysis offers various approaches and combinations that can yield accurate results. However, upon analyzing different projects, it becomes evident that limitations arise when the input signal comprises multiple simultaneous sounds rather than a single waveform.
To overcome the challenge of analyzing complex instruments like the Hackbrett, I have reached a possible realization for the upcoming developing time. When dealing with instruments that produce overlapping sound sources, such as multiple strings being played simultaneously, it becomes essential to implement a specialized approach to improve the accuracy and reliability of the analysis.
One effective solution involves recording each string separately and isolating their individual signals. Moreover, since we already know the frequencies associated with each string, we can leverage this information to our advantage by applying a “third-octave filter”[2] at the input stage to attenuate any potential interferences arising from other strings.
After researching about the topics, I encountered one project made at the IEM by Winfried Ritsch about acoustic of music instruments, the “IAAI[3]”:
“The basic idea is to use the acoustics of the instrument as an instrument, for example as part of a feedback loop. In the acoustics of an instrument, we consider the entire signal path, from the excitation of the strings to the radiation, so pickups in combination with loudspeakers and magnetic actuators for vibrating strings are also part of the acoustic system of the instrument”
Even though the purpose of this research is focused on other aspects, it shows an implementation of technics that fit to my research about finding the best way to detect the pitch.
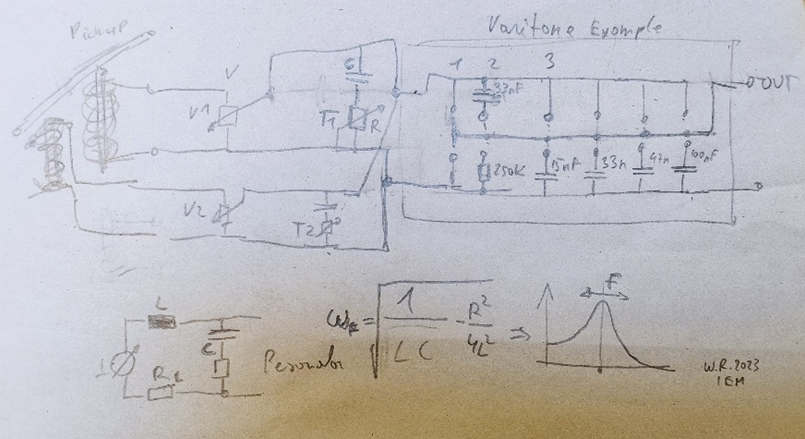
In the specific, the idea of using the “Varitone”[4] to build resonant filters.
The “Varitone” is an electronic circuit found in electric guitars that alters the sound by changing the frequency response. It uses capacitors and resistors connected to the guitar’s pickups to create a low-pass filter network. A rotary switch on the “Varitone” circuit selects different capacitor and resistor combinations, changing the cutoff frequency of the filter.
Rotating the “Varitone” switch modifies the circuit’s capacitors and resistors, which adjusts the cutoff frequency. This affects the amount of treble reduction, resulting in different tones. By passing the guitar signal through various capacitor and resistor combinations, the circuit modifies the frequency response, impacting the amount of high-frequency content reaching the amplifier and creating tonal variations. Since the principle of this system consists precisely in obtaining filters that can be set to different frequencies, I thought of combining this technique for a system of piezo microphones positioned on the instrument.
In the Fig. 8, a draft made by Professor Ritsch that represent the electronics of this system.
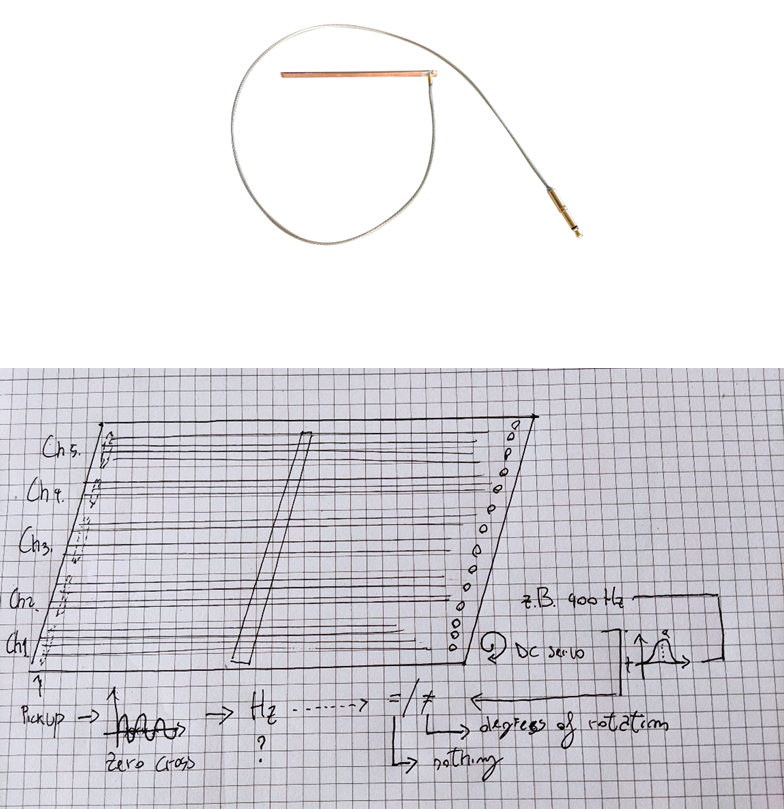
Once the strategy of how to apply the electronics to filter the input signal has been analyzed, I moved on asking myself how to record the signal coming from each string. Here two approaches that I have identified as possible solutions to record the strings separately:
- handmade pickups made by ferrites;

- elastic pickups (Fig. 11) that I used in the past to build guitars and positioning them underneath each choir of the Hackbrett. The advantage of using this piezo is that I could cut them into small pieces and make different microphones from one stick. As we can see in the Fig. 10, I divide the strings into channels to be sent to the pitch detector. Once the analysis is done, I compare the outcoming frequency with the given one of the string to adjust then the servo motor.
[1] Daoo, R. (2020) Algorithmic frequency/pitch detection series – part 1: Making a simple pitch tracker using zero…, Medium. Available at: https://medium.com/the-seekers-project/algorithmic-frequency-pitch-detection-series-part-1-making-a-simple-pitch-tracker-using-zero-9991327897a4 (Accessed: 09 June 2023).
[2] Third-octave filter banks. Available at: https://ccrma.stanford.edu/realsimple/aud_fb/Third_Octave_Filter_Banks.html (Accessed: 09 June 2023).
[3] Ritsch, Windried (no date) Imle, iemCloud. Available at: https://cloud.iem.at/index.php/s/oXcznxBe2TMmZbn?dir=undefined&path=%2FIAAI%2Fdoku&openfile=2966930 (Accessed: 16 June 2023).
[4] Selmer Varitone (no date) TCGAKKI. Available at: https://tcgakki.com/en/pages/selmer-varitone (Accessed: 16 June 2023).